Which of the following statements is true for the system \(\ 2 x-y=-3\) and \(\ y=4 x-1\)? Because the lines are not the same, the equations are independent. Recall that intersecting lines have one solution and therefore the system is consistent. This means the lines intersect at one point-the y-intercept. The two lines in this system have different slopes and the same value for \(\ b\). The lines are identical so the equations are dependent. Since there are many solutions, this system is consistent. The two lines in this system are the same \(\ 3 x+y=-1\) can be rewritten as \(\ y=-3 x-1\).
And because the lines are not the same, the equations are independent.
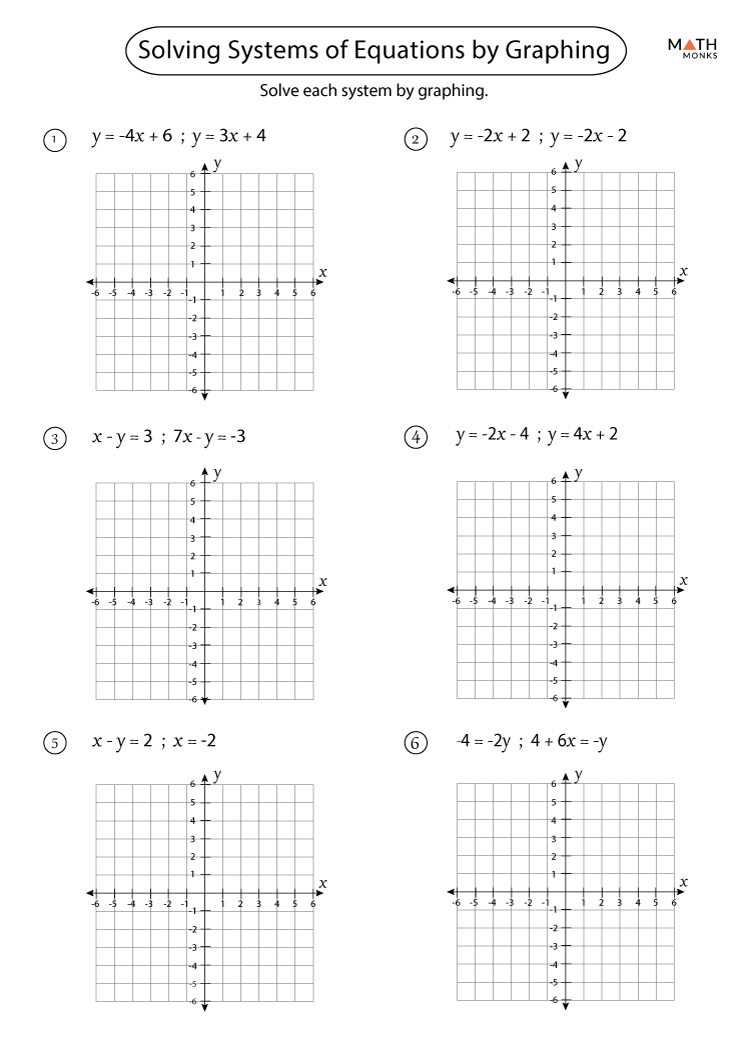
Since there is a solution, this system is consistent. This means the lines intersect at one point. The two lines in this system have different slopes and different values for \(\ b\). The lines don’t intersect, so there are no solutions and the system is inconsistent. The two lines in this system have the same slope, but different values for \(\ b\). Which of the following represents dependent equations and consistent systems? The system is an inconsistent system of linear equations when it has no solutions.The system is a consistent system of linear equations when it has solutions.The following terms refer to whether the system has any solutions at all. That is, any solution of one equation must also be a solution of the other, so the equations depend on each other.
If the lines are the same (the graphs intersect at all points), the system is a consistent system of linear equations and the equations are dependent. When a system has no solution (the graphs of the equations don’t intersect at all), the system is an inconsistent system of linear equations and the equations are independent. When a system has one solution (the graphs of the equations intersect once), the system is a consistent system of linear equations and the equations are independent. The following terms refer to how many solutions the system has. Special terms are sometimes used to describe these kinds of systems. Sometimes the two equations will graph as the same line, in which case we have an infinite number of solutions. When the lines are parallel, there are no solutions. When the lines intersect, the point of intersection is the only point that the two graphs have in common, so the coordinates of that point are the solution for the two variables used in the equations. If the graphs of the equations are the same, then there are an infinite number of solutions that are true for both equations. If the graphs of the equations do not intersect (for example, if they are parallel), then there are no solutions that are true for both equations. If the graphs of the equations intersect, then there is one solution that is true for both equations. Each shows two lines that make up a system of equations. The graphs of equations within a system can tell you how many solutions exist for that system. The solution for a system of equations is the value or values that are true for all equations in the system.
0 kommentar(er)
